Variance and standard deviation are closely related statistical measures that quantify the spread or dispersion of data in a dataset. Both variance and standard deviation expressed as square unit and give the access from square difference of mean. Together, these measures play essential roles in analyzing and interpreting the distribution of data in various fields.
In this article we will discuss standard deviation and variance difference in detail. We will also go over the formulas for variance and standard deviation and thoroughly examine both comparisons using a chart. Furthermore, we will discuss the difference with the help of a table. At the end of this article, we will discuss the concept with the help of detailed example and their solution.
Table of Contents
Concept of Variance
Variance is a statistical measurement also, used to quantify the degree of data dispersion or spread. By using this formula, we find easily variance.
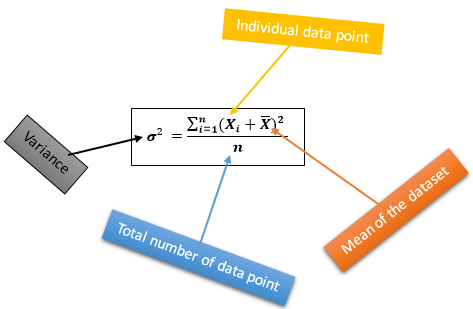
Concept of Standard Deviation
The symbol (σ²) denote the standard deviation and it is also, expressed as the same units of original data value.
By using the following formula, we easily determine the standard deviation.
σ = √σ²
Simply standard deviation called the square root of variance.
Standard deviation and variance: Compression chart
The main difference is the measurement unit. We determine the variance by taking the square of the original unit, making it less interpretable, especially in those cases when we compare the different unit data sets. Let’s suppose we measure the height of an individual’s data sets in centimeters. So, we simply call the variance the square of centimeters and the standard deviation is the original or regular centimeter.
Compression Chart
| Variance | Standard Deviation | |
|---|---|---|
| How Is It Expressed? | Square of average of each data points is called variance. | The standard deviation expressed the same as the unit of the data sets. |
| What Does it Mean? | The mean of variance aver average degree change over time. | low standard deviation shows low volatility and on the other hand high standard deviation represents higher volatility. |
| Meaning | Variance measures the average extent to which individual data points deviate from the mean, indicating the degree of dispersion within a dataset. | Meaning of standard deviation, the average of each data points and mean also, providing a concise indicator of data dispersion. |
| Indicated symbol | Square of sigma (σ²) | Sigma (σ) |
Difference Between Variance and Standard Deviation
The key differences between standard deviation and variance are given below:
| Aspect | Variance | Standard Deviation |
|---|---|---|
| Calculation units | σ2 = ∑ni=1 (Xi – X)2/n | σ = √σ2 |
| Measurement units | Squared units (e.g., square centimeters, square dollars) | Same units as the original data (e.g., centimeters, dollars) |
| Interpretation | Represents the average squared deviation from the mean | Represents the average distance from the mean, in original units |
| Sensitivity to Outliers | Sensitive, as it involves squaring differences | Less sensitive, as it involves the square root |
| Comparative Ease | Less intuitive due to squared units. | More intuitive, expressed in original units. |
| Applications | Widely used in statistical analyses and calculations | Commonly used for practical interpretation and communication |
Both variance and standard deviation measure the data of dispersions, the key difference lies in their units, interpretation, and sensitivity to outliers. Variance uses squared units and is more sensitive to extreme values, making standard deviation, with its original units, often preferable for practical understanding and communication of data variability.
Example Section
Example 01:
Suppose the seven subject scores of students are 50, 78, 88, 75, 95, 60 and 55. Variance and standard deviation=?
Solution
Given data are:
50, 78, 88, 75, 95, 60 and 55
Step 01:
Determine the mean
Mean = 50 + 78 + 88 + 75 + 95 + 60 + 55 / 7 Mean = 501/7 Mean = 71.57
Step 02:
Now we find the variance of the given data:
| X | A | X-A | (X-A)2 |
|---|---|---|---|
| 50 | 71.57 | 50-71.57 = -21.57 | 465.2649 |
| 78 | 71.57 | 78-71.57 = 6.43 | 41.3449 |
| 88 | 71.57 | 88-71.57= 16.43 | 269.9449 |
| 75 | 71.57 | 75- 71.57= 3.43 | 11.7649 |
| 95 | 71.57 | 95-71.57 = 23.43 | 548.9649 |
| 60 | 71.57 | 60-71.57 = -11.57 | 133.8649 |
| 55 | 71.57 | 55-71.57 = -16.57 | 274.5649 |
Here, X is the observation and A is the Arithmetic mean.
Step 03:
Evaluate the variance
Variance = ∑(X-A)2/7 Variance = 1747.7143 /7 Variance = 249.67
Step 04:
Evaluate the standard deviation
σ = Square root of variance σ =√249.67 σ = 15.801
The problems of finding variance and standard deviation can also be solved with the help of a standard deviation calculator.
Example Number 02:
Let’s suppose a die is rolled, then determine the variance and standard deviation of possible outcomes.
Solution:
When a die is rolled 6 possible outcomes will have come. So, sample data sets = 1,2,3,4,5,6 and total sample space n= 6
For determining variance
Step 01:
Evaluate the mean of sample data
Mean = (1+ 2+ 3+ 4+5+6)/6 Mean = 3.5
| X | A | X-A | (X-A)2 |
|---|---|---|---|
| 1 | 3.5 | 1-3.5 =-2.5 | 6.25 |
| 2 | 3.5 | 2-3.5 = -1.5 | 2.25 |
| 3 | 3.5 | 3-3.5 = -0.5 | 0.25 |
| 4 | 3.5 | 4-3.5 = 0.5 | 0.25 |
| 5 | 3.5 | 5-3.5 = 1.5 | 2.25 |
| 6 | 3.5 | 6-3.5 = 2.5 | 6.25 |
Step 02:
Determine the variance
σ2 = ∑ (X-A)2 /6 Variance = 2.917
Step 03:
Determine the standard deviation
σ2 = √σ2 Standard deviation = 1.708
Summary
In this article, we have discussed standard deviation and variance difference in detail. We have also covered the formulas for variance and standard deviation and have thoroughly examined the comparisons between the two with the aid of a chart.
Additionally, we have used the table to help us discuss the differences. By the time this article ends, we have thoroughly covered both ideas with the aid of real-world examples. We hope you will be able to defend this article anywhere after completely understanding this article.
FAQs
What is the practical significance of standard deviation and variance in finance?
Answer: To determine the degree of return volatility on investments Variance and standard deviation are used. Lower values indicate more consistent and predictable returns, while higher values indicate riskier investments with greater fluctuations.
How are standard deviation and variance used to control for quality and process of manufacturing?
Answer: In quality control, variance is used to assess the consistency and stability of manufacturing processes. Low variance indicates a more consistent output, while high variance may signal variability and potential quality issues.
Why is standard deviation often preferred for interpretation?
Answer: When analyzing data, standard deviation is preferred over squared units of variance because it is expressed in the original units of the data, making it easier to understand and apply.


