If you divide an object into smaller pieces, you must have a way to describe what each part is. For instance, you can split a pie into two equal halves by cutting it in half. The entire pie is made up of the two halves.
This can be expressed mathematically as:
1/2 +1/2 =1
The pie can also be divided into three equal portions or thirds. The entire pie is made up of thirds. For this, you can also create another mathematical expression.
The mathematical representation of a portion of a whole is known as a fraction.
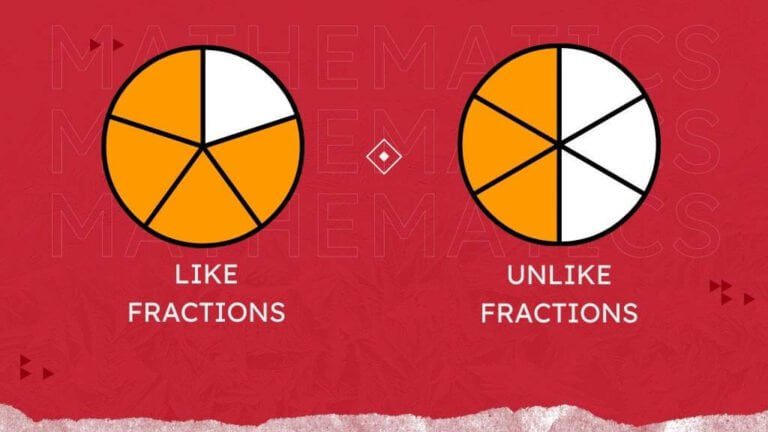
Fractions can be divided into two groups: like fractions and unlike fractions. Based on the denominators, fractions are categorized as like or unlike.
Accordingly, the difference between like and unlike fractions is that the former refers to sets of two or more fractions with the same denominator, whilst the latter refers to sets of two fractions with different denominators.
Let’s understand the definition of like and unlike fractions
Table of Contents
What are Like Fractions?

When the denominator of two or more fractions or a collection of fractions is the same, these are said to be like fractions. However, the bottom of all fractions has the same number.
Like fractions examples include:
a) 1/5, 3/5, 5/5, 7/5 and 9/5
b) 1/2, 3/2, 5/2, 7/2 and 9/2.
Since all of these fractions have 5 and 2, as their common denominator, they are referred to as, like fractions.
What are Unlike Fractions?

When two or more fractions have distinct denominators, the denominators are referred to as, unlike fractions.
In other words, the bottom of the fraction bar needs to have different numbers.
Unlike fractions, example include:
a) 1/2, 2/4, 3/5, 5/9 and 7/6.
2) 2/6, 3/9, 4/8, 5/2 and 6/3.
The denominators of the fractions mentioned above are different.
How Unlike Fractions are Identified?
We say given fractions are unlike fractions when two fractions are compared and they have a distinct denominator.
Alternatively said, fractions with different denominators are referred to as unlike fractions. It also goes by the name, unlike denominators.
Adding and Subtracting Like Fraction and Unlike Fraction
The definitions given above help us understand the difference between like and unlike fractions.
The difference between like and unlike fractions will be crucial when adding and subtracting fractions.
1) When adding two or more similar fractions, we just need to take the denominator once to simplify the numerators.
Example:
3/9 + 5/9 = (3+5)/9
3/9 + 5/9 = 8/9
It is evident from the example above that adding or subtracting two or more fractions that are similar is simple.
2) However, we need to use various techniques when adding or subtracting two or more unlike fractions.
These are,
1. Cross-Multiplication Method
2. L.C.M. Method
1) Cross-Multiplication Method

Cross multiplication is multiplying the left fraction’s numerator by the right fraction’s denominator in an equation and setting the result equal to the right fraction’s numerator by the left fraction’s numerator.
If the denominators of two, unlike fractions, are co-prime or nearly prime, we must use this method when adding or subtracting them.
In order to use the cross-multiplication method, we must follow the steps listed below.
Step 1
Multiply the denominator of the second fraction by the numerator of the first fraction.
Step 2
Multiply the first fraction’s denominator by the second fraction’s numerator to get the answer.
Step 3
To find the common denominator for the outcomes of steps 1 and 2, multiply the denominators of the two fractions.
Example:
Let’s think about adding the two fractions shown below.
5/6 + 6/7
The denominators of the two fractions above are 6 and 7.
There is only one common divisor for the numbers 6 and 7-1.
6 and 7 are hence co-prime.
Here, as seen below, we must add the two fractions 5/6 and 6/7 using the cross-multiplication method.
5/6 + 6/7 = [(5⋅ 7) + (6 ⋅ 6)] / (6 ⋅ 7)
5/6 + 6/7 = [35 + 36] / (42)
5/6 + 6/7 = 71/42
2. Least Common Multiple (L.C.M.) Method

A method to determine the smallest common multiple between two or more numbers is called the least common multiple (L.C.M.).
When adding or subtracting two unlike fractions, we must use this method if the denominators are not co-primes (there is a common divisor other than 1).
We must follow the L.C.M. method’s listed steps.
Step 1
Find the fractions’ denominators with the lowest common multiple.
Step 2
Make all the fractions similar by using the least common multiple that was determined in step 1.
Step 3
The denominator of all fractions in like fractions will be the same. Therefore, simplify the numerators by taking the denominator only once.
Example:
Let’s think about adding the two fractions shown below:
3/8 + 5/12
The denominators of the two fractions above are 8 and 12.
If there is at least one common divisor for the numbers 8 and 12 besides 1, then these numbers are not co-primes.
The following common divisors, except 1, exist for the numbers 8 and 12 are 2 and 4.
Thus, 8 and 12 are not co-primes.
The L.C.M. (Least Common Multiple) of 8 and 12 must be found in the following step.
8 = 23
12 = 22 x 3
8 and 12 have the prime factors 2 and 3 when we divide them into prime numbers.
We must combine the maximal powers of 2 and 3 to obtain L.C.M. of 8 and 12.
The L.C.M. of 8 and 12 is thus:
= 23 x 3
= 8 x 3
= 24
Use multiplication to change the denominators of both fractions to 24.
Multiply the numerator and denominator of the first fraction by 3 and the second by 2 to make each denominator equal 24 in (3/8 + 5/12).
That is,
3/8 + 5/12 = 9/24 + 10/24
3/8 + 5/12 = (9 + 10)/24
3/8 + 5/12 = 19/24
What are the Differences Between Like and Unlike Fractions?

Highlighting the main differences between like and unlike fractions in the following table:
Conclusion
Therefore, a fraction is a number that represents a portion of a single whole thing. It is defined by two numbers, the numerator, and denominator, located at the top and bottom of a fraction bar, respectively. We have two fractions that are like and unlike fractions depending on how similarly, and severely the denominators differ.
The difference between like and unlike fractions is that like fractions have the same denominators, while unlike fractions have different denominators.
Read more: What is the Difference Between Area and Perimeter?