You must first learn the concept of a function to understand the difference between a function’s differential and derivative.
One of the fundamental ideas in mathematics is the concept of a function, which describes the connection between a set of inputs and a set of potential outputs, where each input connects to one output. The independent variable is one variable, and the dependent variable is another.
In mathematics, variables are any physically altering entities. The difference between the differential and derivative is that if there is a change in the rate of one variable for another variable, we refer to it as a derivative.
On the other hand, a differential equation is a corresponding equation that expresses the relationship between variables mathematically.
Let us learn the basic definitions and difference between the differential and derivative:
Table of Contents
What is Derivative?

The speed at which a function changes at a specific instant in time is called a derivative.
For instance, a line’s slope, which determines its rate of change, is constant along the entire line. The derivative informs us what the slope of a parabola is at a specific point because the slope of a parabola fluctuates.
Another way to depict a derivative is to use the slope of a line that is drawn tangent to a curve at a certain point. Taking a derivative is the process of differentiating. Differential equations and derivatives are frequently used together.
Finding derivatives is done through the differentiation process. They are used to denote a tangent line’s slope. Derivatives quantify the steepness of the slope of a function over a specified time interval.
Derivative of an Integral
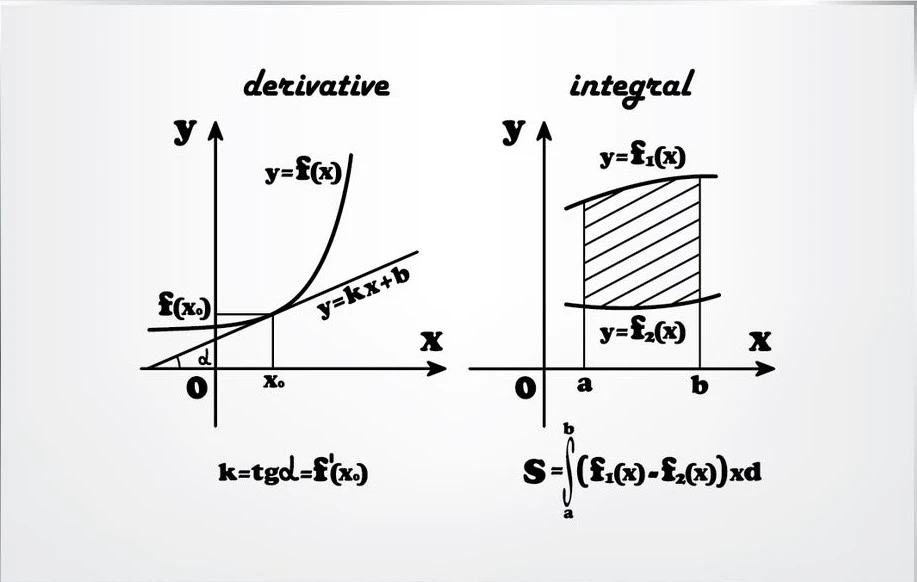
The outcome of differentiating an integral’s result is the derivative of an integral. Since differentiation of an integral should provide the original function itself, integration is the process of locating the “anti” derivative.
When the integral’s lower limit is a constant and its upper limit is just a variable, its derivative is the function itself. In other words, where “a” is a constant, d/dx ∫ax f(t) dt = f(x).
Read more: What is the Difference Between Like and Unlike Fractions?
What is Differential?
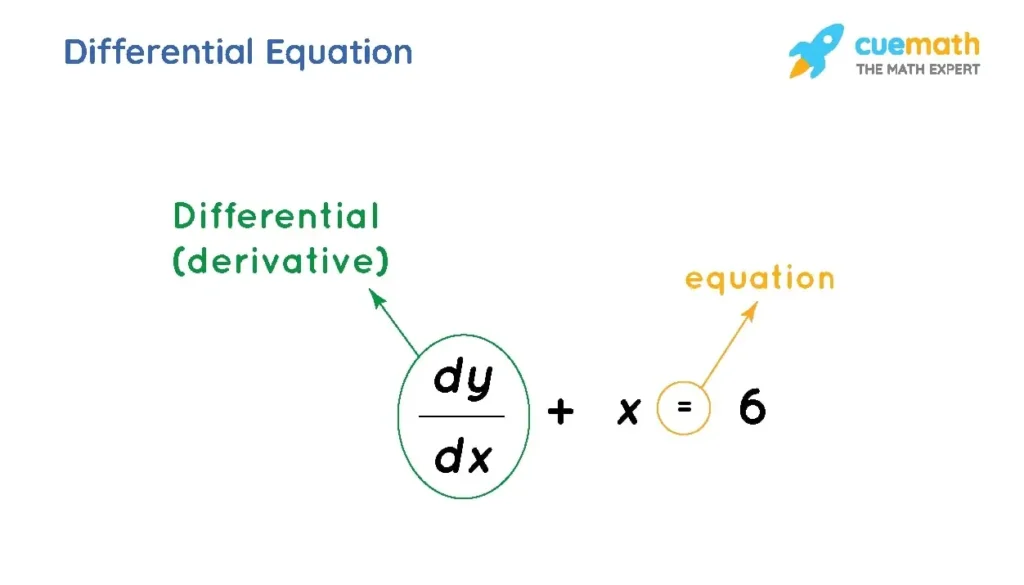
Differential equations are a calculus branch that depicts the slightest variation in some variable quantities. Derivatives and their functions are part of differential equations.
Calculus’ fundamental divisions include the differential and integral branches. The environment we live in is full of constantly changing, interconnected quantities.
The symbol for a differential, an infinitesimally small amount, is often dy/dx.
Because a derivative reflects the slope of a function on an infinitesimally short interval comparable to a single point, it is frequently thought of as a quotient of differentials, such as dy/dx, dy/dx.
Difference Between the Differential and Derivative
The main between the differential and derivative given below:
The primary difference between the differential and derivative is that a derivative refers to the rate of a function’s change, but a differential refers to the actual change in the function.
Another way to define derivatives is to consider the ratio of the function and variable differentials.
Another difference between the differential and derivative is that a differential is a change in a variable (dx). In contrast, a derivative is a change in a function (dy/dx) (dy/dx) (dx).
The derivative is a ratio of differentials because a function represents the relationship between two variables. Differentials indicate the actual value change through a linear map, whereas derivatives represent the same change through a slope map.
Differential Vs. Derivative
In terms of relationships, the terms differential and derivative are closely related to one another. Variables are changing objects in mathematics, and the rate at which one variable changes in relation to another is known as a derivative.
Differential equations describe the relationship between these variables and their derivatives. Finding a derivative is the process of differentiation.
The comparison between differential vs. derivative is that the differential of a function is the actual change in the function, whereas the derivative is the rate at which the output value changes in relation to the input value.
Representation of Differential Vs. Derivative
Differentials can be represented as dx, dy, and so on, where dx represents a small change in x, dy represents a small change in y. The differential dy can be expressed as follows when contrasting changes in related values where y is a function of x:
A function’s slope at any given point is its derivative and can be represented as d/dx.
For example, we can write the derivative of sin(x) as:
d/dx sin(x) = sin(x)’ = cos(x)
Relationship Between Derivative and Differential
Differentiation is a technique for calculating a derivative or the rate at which the output y of a function changes as a function of the changing variable x.
Simply put, a derivative is a rate at which y changes about x.
This relationship represents y = f(x), which denotes that y is a function of x.
The function whose value generates the slope of the function f(x) where it is specified and f(x) is differentiable is said to be the derivative of f(x). It speaks of the graph’s slope at a specific location.
What is the Difference Between the Differential and Derivative?
Highlighting the main difference between the differential and derivative in the following table:
| Derivative | Differential |
|---|---|
| The rate of change of the variables in a differential equation is represented by derivatives. | Differentials indicate the smallest variations in variables’ quantities. |
| The slope of the graph at a particular point is calculated. | It is calculated to find the linear difference. |
| Simple derivatives merely indicate how quickly the dependent variable is changing in relation to the independent variable. | Derivatives are a tool used in the solution of differential equations. Differential equations have derivatives as well. |
| It is known how different variables relate functionally. | There are no known functional relationships between the variables. |
| There are many derivative degrees and different representational formulae. The formula for a derivative that is most frequently employed is: d/dx | Numerous formulas can be used to express differential equations. One of the most used formulas is: dy/dx = f. (x) |
Conclusion
A differential and a derivative differ in terms of the functions they execute and the values they each represent. The difference between the differential and derivative is that differentials describe minor variations in varying amounts, such as the area of a body.
It makes it possible to compute the equation’s dependent and independent variable relationships.
Learn more: What is the Difference Between Area and Perimeter?


